Cześć Pierwsza
Do czego służy Povray
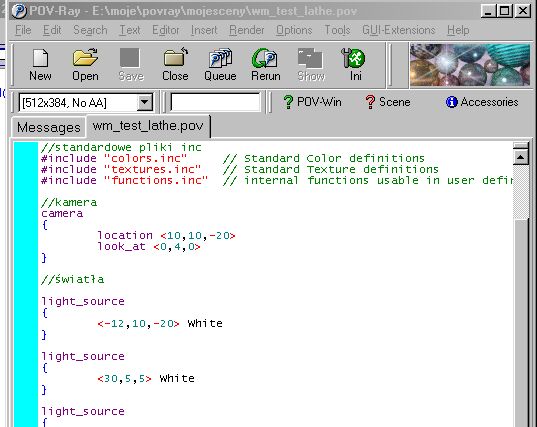
Na powyższe pytanie można odpowiedzieć jednym zdaniem - do tworzenia grafiki 3D - zarówno obrazów statycznych jak i animacji. Być może nie wszyscy jednak wiedzą na czym polega ten szczególny rodzaj grafiki. W skrócie można to przedstawić tak: tworzymy scenę zawierającą obiekty przestrzenne, pokryte różnorodnymi materiałami, światła i kamerę, w której powstanie obraz. Tak przygotowaną scenę poddaje się procesowi zwanemu renderingiem. W jego trakcie komputer oblicza jak biegną promienie od źródeł, co się dzieje, gdy świało pada na powierzchnie obiektów i co widzi kamera. W wyniku powstaje płaski obraz trójwymiarowego świata. Raz przygotowaną scenę możemy oglądać z różnych miejsc, przy pomocy kamer o różnych parametrach. Możliwe jest także utworzenie animacji zamiast obrazów statycznych. Efekty pracy artystów zajmuujących się gbrafiką 3D obserwować możecie w postaci efektów specjalnych w wielu filmach.Program Povray jest jednym z wielu programów do tworzenia fotorealistycznych obrazów symulujących trójwymiarowe sceny i animacje. Można powiedzieć, że Povray pod tym względem należy do licznej rodziny programów wśród których można wymienić choćby 3DStudio Max, Maya, Lightwave, Realsoft3D, Cinema4D i wiele wiele innych programów. Od wymienionych powyżej różni się jednak zasadniczo: sceny tworzymy opisując występujące w nich obiekty przy użyciu języka programowania. Poniższy rysunek przedstawia fragment kodu sceny napisanej w programie Povray.
|
Inną cechą odróżniającą Povray od wymienionych wyżej programów jest to, iż jest on całkowicie darmowy. Znaleźć go można w wielu miejscach w sieci a jego stroną domową jest www.povray.org. Najnowsza wersja ma numer 3.50. Jest dostępna na wszystkie znane mi platformy sprzętowe i systemowe - dla Windows, Linux-a, Max OS, Mac OS X. Ja pisząc te materiały używam wersji dla Windows i wszystkie rysunki i opisy pochodzą z tej wersji.
Ze względu na sposób tworzenia sceny nie jest to program najłatwiejszy, ma jednak wiele cech, które powodują, że posiada zwolenników na całym świecie. Autorzy podają, że w ciągu roku pobierany jest 100 000 razy. Niewątpliwie jest świetnym narzędziem do ćwiczenia wyobraźni przestrzennej. Napisano wiele dodatkowych programów współpracujących z Povray-em. Są to edytory scen i tekstur, programy ułatwiające deformację obiektów, konwertujące zbiory klatek do plików filmowych.
Zaczynamy pracę z programem
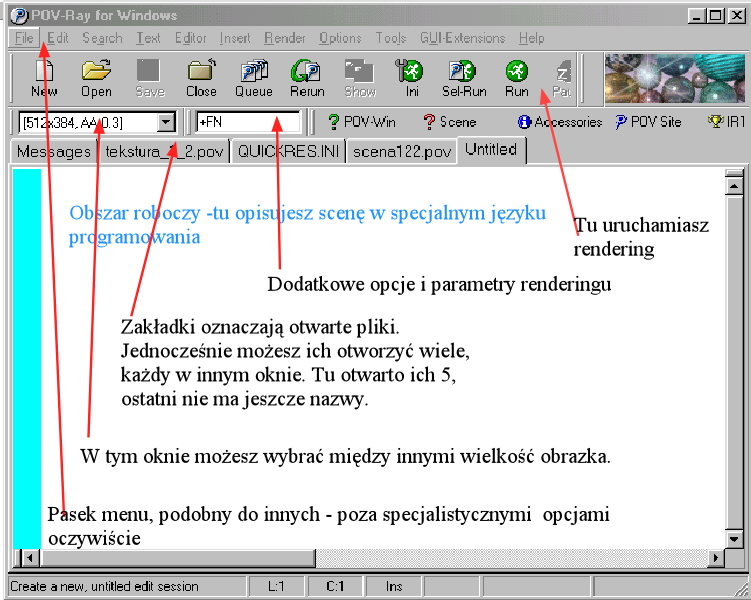
Zanim utworzymy jakąkolwiek scenę spróbujmy najpierw wykorzystać jedną z gotowych scen przykładowych dołączonych do programu. Najpierw jednak rzućmy okiem na interfejs programu
|
Aby rozpocząć pracę z nowym plikiem wybieramy z menu File/Open File. W otwartym standardowym oknie dialogowym odszukajmy katalog scenes\advanced\fish13 a w nm plik fish13.pov i otwórzmy go. W oknie roboczym pojawi się tekst sceny. Proponuję niczego w nim nie zmieniać. Uruchamiamy rendering wciskając przycisk Run na pasku narzędziowym i obserwujemy efekt. Musimy trochę poczekać bo celowo wybrałem dosyć skomplikowaną scenę. Jeśli obrazek jest za mały wybieramy inny rozmiar w odpowiednim miejscu interfejsu - patrz rysunek 2.
Jak Povray widzi świat
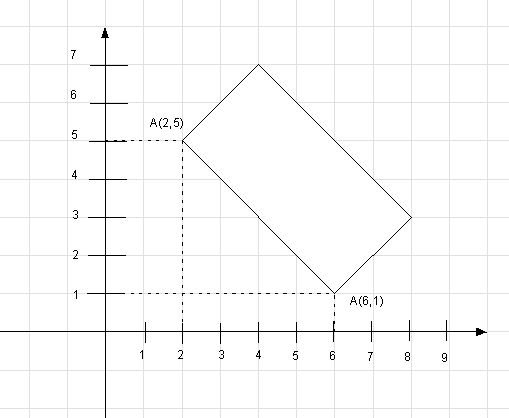
Musimy zacząć od przypomnienia pewnych niezbędnych wiadomości z matematyki. Narysuj na kartce papieru prostokąt. Wyznaczają go cztery punkty stanowiące jego wierzchołek. Aby precyzyjnie opisać położenie naszego prostokąta musimy użyć układu współrzędnych. Jeśli podamy współrzędne każdego wierzchołka jednoznacznie określimy nie tylko położenie prostojkąta ale także jego wielkość. Gdybyśmy podali te współrzędne innej osobie może ona dokładnie odtworzyć cały nasz prostokąt. Rysunek poniżej przypomina jak definiujemy współrzędne punktu na płaszczyznie posługując się płaskim układem współrzędnych.
|
| Rys. 3 Współrzędne płaskie |
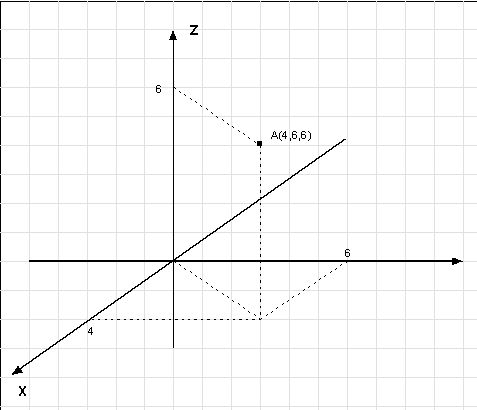
Budując sceny w Povray-u tworzymy bryły, które mają, podobnie do rzeczywistych obiektów, trzy wymiary. Dwie osie płaskiego układu współrzędnych nie wystarczą do określenia położenia puntów składających się na te obiekty. Musimy użyć układu trójwymiarowego. Taki układ składa się z trzech wzajemnie prostopadłych osi : X, Y i Z. Na rysunku poniżej pokazano jak określa się współrzędne punktów w przestrzeni.
|
| Rys. 4 Określanie współrzędnych punktu w przestrzeni przy użyciu trójwymiarowego układu |
Narysowana w rzucie oś X w rzeczywistości powinna wchodzić w kartkę ( lub ekran monitora) prostopadle. W programie Povray używamy inaczej ustawionych osi. Jeśli patrzysz na ekran oś X skierowana jest w prawo, oś Y do góry a oś Z wchodzi w ekran - punkty o dodatnich współrzędnych są "wewnątrz" monitora a punkty położone pomiędzy tobą a monitorem mają wspólrzędne z ujemne. Na rysunku wygląda to tak:
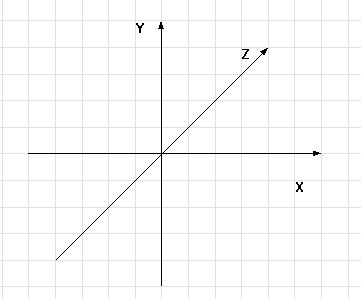
|
| Rys. 5 Układ osi używany przez program Povray |
Pierwsza scena
Komentarze
Przy pisaniu jakichkolwiek programów dobrym zwyczajem jest opisywanie poszczególnych fragmentów tak, aby wiadomo było do czego służą. Znaczenie komentarzy docenią ci, którzy powracają do programu po jakimś czasie od jego napisania lub szukają w programie błędów. Tekst komentarza jest ignorowany przy tworzeniu sceny przez Povray. Komentarze umieszczamy w następujący sposób:Zaczynamy pisać pierwszą scenę od opisu. Z menu File wybieramy polecenie New i wpisujemy: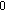
//to jest tekst komentarza
lub
/* tu zaczyna się komentarz
tu ciągnie się dalej
a tu się kończy*/
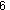
Oczywiście możesz wpisać inne informacje, zadbaj jednak o to aby coś mówiły o tworzonym pliku.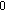
//Wojciech Mickiewicz
//2002-04-03
//moja pierwsza scena w Povray-u
Zaczynamy tworzyć scenę
Teraz wpiszemy trzy linijki, których znaczenie omówię za chwilę.Polecenia zapisane powyżej powodują, że do naszej sceny dołączamy pliki o nazwach podanych w cudzysłowie. Oczywiście równie dobrze można byłoby te pliki po prostu przepisać, lub nawet korzystając z funkcji kopiuj i wklej wstawić bezpośrednio do naszej sceny. Podany tu sposób jest jednak znacznie wygodniejszy a długość naszego pliku znacznie krótsza - co ułatwi jego przeglądanie i analizę. Zawartość dołączanych plików bardzo nam się niebawem przyda. Pierwszy z nich - colors.inc -zawiera zdefiniowane kolory, dzięki niemu jeśli coś ma być niebieskie to wpiszemy po prostu Blue a jeśli czerwone to Red. Drugi plik - shapes.inc zawiera podstawowe bryły, nie będziemy musieli definiować kuli czy walca - już są zdefiniowane. Trzeci plik textures.inc zawiera tekstury a co to jest - opowiemy dalej.
#include "colors.inc"
#include "shapes.inc"
#include "textures.inc"
Do utworzenia sceny potrzebne są:
- Obiekty tworzące elementy widzialne sceny - modele
- ¬ródła światła, które oświetlą scenę
- Kamerę, która pozwoli cokolwiek zobaczyć.
Dodajemy kamerę
Zaczniemy od kamery. Ustawmy w punkcie o współrzędnych (0,10,-15) i niech będzie skierowasna na punkt (0,0,0). Przypomnij sobie jak ustawione są osie układu współrzędnych wykorzystywanego przez Povray-a i zastanów się gdzie znajdują się wymienione punkty. Kamerą wpisujemy tak:
camera {
location <0,10,-15> // miejsce umieszczenia kamery
look_at <0,0,0> // punkt na który kamera jest skierowana
}
Oświetlenie sceny
Teraz czas na źródła światła. Umieścimy dwa punktowe źródła emitujące światło białe.poćwicz trochę wyobraźnie i postaraj się odpowiedzieć na pytanie: jak względem kamery położone są światła?
light_source
{
<-10,10,-10> White
}
light_source
{
<3,20,5> White
}
Właśnie utworzyliśmy coś co może stanowić szablon sceny do dalszych ćwiczeń. Zapiszmy go więc pod nazwą szablon.pov. Nie będziemy musieli za każdym razem pisać wszystkiego od początku.
Pierwsza bryła
Teraz kolej na bryły tworzące obiekty widzialne sceny. Na początek umieścimy w punkcie (0,0,0) kulę o promieniu 2. Pomalujmy ją na czerwono.Jak zauważyłeś kolor możemy podać określając jego składowe w podstawowych barwach modelu RGB. Ten sam efekt otrzymamy pisząc: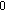
sphere
{
<0,0,0>, //położenie środka kuli
2 // promień kuli
texture {pigment {color red 1 green 0 blue 0}}
}
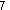
udział każdego z kolorów bazowych określamy liczbą z zakresu od 0 do 1.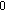
texture {pigment {color rgb <1,0,0>}}
Rendering
Jeśli już wszystko wpisałeś do pliku zapisz go pod nazwa scena1.pov i uruchom rendering wciskając na pasku narzędziowym przycisk Run. Teraz poczekaj chwilę na efekt. A oto on:

|
Linijka ta zaczyna się od słowa kluczowego texture Wszystko to co jest zawarte pomiędzy klamrowymi nawiasami za tym słowem opisuje teksturę czyli najprościej mówiąc materiał, którym pokryty jest obiekt. Będzie o tym mowa w dlaszej części. Część opisu tekstury decyduje o tym jakim kolorem (kolorami) będzie pokryty obiekt. Decyduje o tym zawarta w klamrowych nawiasach po słowie kluczowym pigment. W naszym przykładzie określiliśmy kolor określając jego skladowe w modelu RGB. Poćwicz stosowanie różnych parametrów. Można też zrobić inaczej. Wiele kolorów zostało utworzonych już wcześniej i zapisanych w pliku Colors.inc, który, jak pamiętasz, dołączyliśmy do naszej sceny. Zajrzymy do tego pliku ale nie bezpośrednio:
texture {pigment {color rgb <1,0,0>}}
- pracując w programie otwórz plik scena1.pov, nastęnie przejdź do pomocy.
- w prawej ramce masz spis treści, odszukaj Standard Include Files kliknij na nim
- z rozwiniętej listy wybierz colors.inc, następnie wskaż Predefined Colors
- w prawej ramce masz pokazaną w wygodny sposób zawartość tego pliku. Wybierz odpowiadający ci kolor i zapisz dokładnie jego nazwę.
- wpisz tę nazwę do pliku opisu sceny po słowie color
- uruchom rendering i podziwiaj efekt.

|
| Rys.6 Układ kul do ćwiczenia 4 |
Część Druga
Trochę szerzej o obiektach
Inne bryły
Niestety kula nie wystarczy do zbudowania zbyt wielu ciekawych scen. W tej części pokażemy jak wprowadzić do naszej sceny inne bryły.Prostopadłościan
Dla zdefiniowania prostopadłościanu potrzebujemy współrzędne dwóch wierzchołków A i B tak jak to pokazano na rysunku:
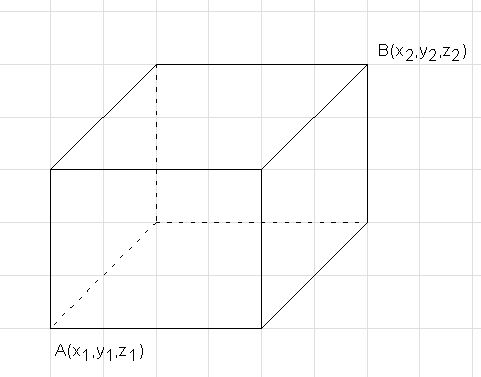
|
| Rys.7 Współrzędne punktów A i B definiują prostopadłościan |
i już mamy w naszej scenie prostopadłościan, który tym razem pomalowałem na niebiesko ale ty możesz wybrać inny kolor. Następne bryły podam już bez zbędnych opisów. Oczywiście kolory mogą być wybrane dowolnie.
box
{
<x1,y1,z1>,
<x2,y2,z2>
texture {pigment {color Blue}}
}
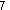
Walec, stożek, torus
|
Opis oznaczeń: A i B - środki podstaw - górnej i dolnej r - promień walca
|
|
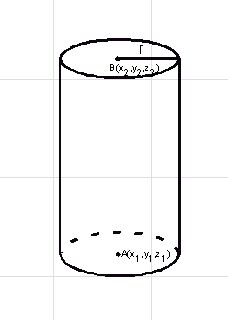
Oznaczenia: A - środek dolnej podstawy r1 - promień dolnej podstawy B - środek górnej podstawy r2 - środek górnej podstawy Jeśli nie chcesz stożka ściętego podaj promień górnej podstawy równy 0 |
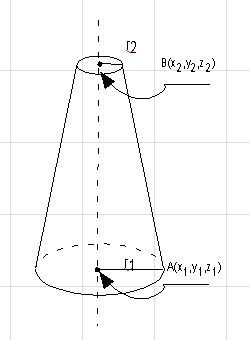
|
Torus wygląda doładnie tak jak napompowana dętka wyjęta z koła rowerowego. Określają go dwa parametry: r1 - odpowiednik promienia koła roweru i r2 - określający promieć przekroju dętki. Aby dodać torus do swojej sceny wpisz:Zwróć uwagę na to, że nie podajemy położenia tej bryły względem układu współrzędnych tylko jej rozmiary.Zbuduj scenę zawierającą tylko torus i osie współrzędnych aby zobaczyć jak program umieścił tę bryłę w przestrzeni. |
Pokazane wyżej obiekty nie wyczerpują wszystkich możliwości programu ale wystarczą do zbudowania dosyć skomplikowanych scen dlatego na nich poprzestanę. O innych możesz poczytać w dokumentacji programu.
Warto w tym miejscu zwrócić uwagę na wymiary obiektów. Do tej pory posługiwaliśmy się jedynie współrzędnymi punktów. Nic jednak nie stoi na przeszkodzie aby przyjąć, że osie naszego układu współrzędnych są wyskalowane w centymetrach i punkt o współrzędnych (100,0,0) znajduje się na osi X w odległości 100 cm od początku układu. Mówiąc zupełnie niefachowo możemy stwierdzić, że współrzędne wyrażone są w centymetrach.
Przy okazji jeszcze jedna uwaga - sceny tworzymy w edytorze tekstów, należy więć jak najszerzej korzystać z tego faktu. Jeśli mamy na przykład umieścić w scenie dwa prostopadłośiany to wpisujemy jeden a potem kopiujemy i wklejamy odpowiedni fragment tekstu i odpowiednio zmieniamy współrzędne. Na koniec tego rozdziału proponuję wykonanie przedstawionych na ilustracjach prostych modeli.
 | Pudełko z trzech walców, nie da się wprawdzie otworzyć ale można wyobrazić sobie, że w środku jest kapelusz |
 | Model lampki nocnej wykonany w walca i dwóch stożków |
 | Wykonany w prostopadłościanów regał. Zauważ, że zawiera on kilka jednakowych brył. Wystarczy napisać jedną i skopiować ją kilka razy przez proste powielanie tekstu a następnie odpowiednio zmienić współrzędne |
 | Do wykonania tej półki potrzeba prostopadłościanów i walców |
 | Prostym złożony z czterech prostopadłościanów stoli. Zakładamy, że stolik został wykonany z płyty o grubości 2 cm a poszczególne elementy mają następujące wymiary:
|
Część Trzecia
Operacje boolowskie
Operacje, które chcę teraz przedstawić znacznie powiększają możliwiości tworzenia bardziej skomplikownaych brył. Zamiast opowiadać o tym na czym polegają operację boolowskie pokażę to na przykładach figur płaskich: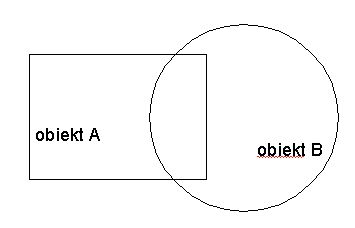 | Mamy dwa obiekty: A i B. Obiekty te częściowo się pokrywają |
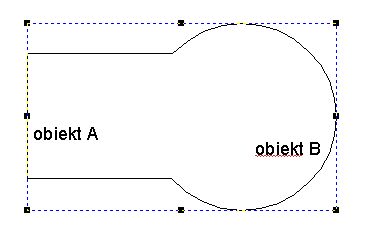 | Operacja Union
Nowy obiekt powstaje przez połączenie obiektów A i B.
|
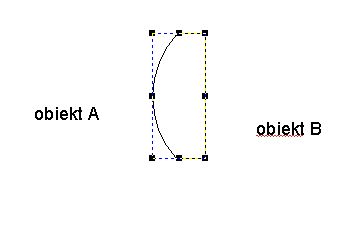 | Operacja Intersection Nowy obiekt jest częścią wspólną obiektów A i B
|
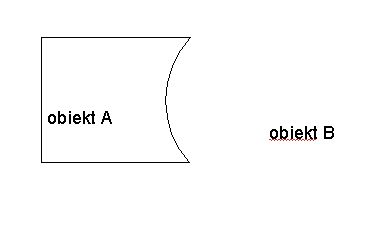 | Operacja difference A-B W tej operacji od obiektu A odejmujemy obiekt B
|
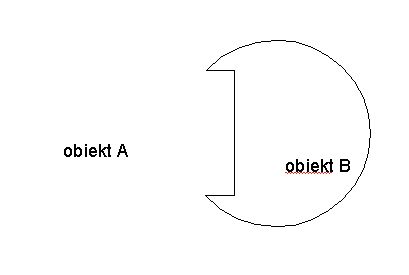 | Operacja difference B-A Tu natomiast od obiektu B odejmujemy obiekt A
|
Tak samo można zastosować operacje boolowskie do brył. Poniżej podaję trzy przykłady.
Operacja union
Połączymy trzy kule tak aby utworzyły bałwana
union // zapis operacji łączenia brył
//pierwsza kula

{
sphere {<0,-1,0>,1.5 pigment {color LightGray}}
//druga kula
sphere {<0,1,0>,1 pigment {color LightGray }}
//trzecia kula
sphere {<0,2.3,0>,0.6 pigment {color LightGray}}
}
A oto efekt:

Efektu operacji union nie widać bezpośrednio w modelu. Efekt jest taki sam jaki uzyskalibyśmy umieszczając te same obiekty osobno. Są jednak sytuacje, w których jest ona potrzebna - na przykład przemieszczanie obiektów.
Operacja difference
Zbudujmy prostą szklankę. Można ją utworzyć przez wycięcie jednego ściętego stożka z drugiego. Na rysunku niżej po lewej widac jak powstanie nasza szklanka a po prawej gotowy efekt: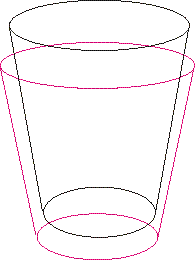 |  |
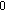
difference //operacja boolowska
{
cone {<0,0,0>,2,<0,8,0>,2.5} //pierwszy stożek
cone {<0,0.5,0>,1.9,<0,9,0>,2.45} //drugi stożek, trochę wyżej i wyższy
pigment {color Blue}
}
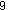
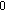
Operacja intersection
Zastosuję tę operację aby uzyskać ćwiartkę kuli. Umieszczę kulę o promieniu 2 w środku układu współrzędnych, Drugą bryłą będzie sześcian o boku 2 umieszczony tak, aby jeden z jego wierzchołków znajdował się w środku kuli.Tak wygląda utworzona bryła: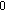
intersection
{
sphere {<0,0,0>,2}
box {<:0,0,0>,<2,2,2>}
pigment {color Scarlet}}

Zwróć uwagę na to, że wewnętrzny stożek musi być trochę wyższy od zeznętrznego. Teraz już możesz wycinac w swoich obiektach otwory i tworzyć najprzeróżniejsze obiekty. Oto kilka przykładów do ćwiczeń:
 | Klocek Lego powstał przez połączenie prostopadłościanu z walcami za pomocą operacji union |
 | Pudełeczko powstanie jeśli w jednego prostopodałościanu wytniemy drugi. Oczywiście potrzebna jest tu operacja difference |
 | Inny przykład operacji difference - ściana narożnik pokoju z trzema oknami. Trzeba tylko dostawić meble. Sam narożnik pokoju powstał za pomocą operacji union dla dwóch prostopadłościanów. Okna wycięto stosująć jeszcze raz tę samą operację, jako bryły do wycięcia posłużyły trzy odpowiednio ustawione prostopadłościany |
 | Bryła przypominająca kształtem kostę do gry utworzona jako część współna sześcianu o boku 4 cm i kuli o promieniu 2.6 umieszczonych w środku układu współrzędnych. Zastosowano oczywiście operację intersection |
Część Czwarta
Podstawowe transformacje obiektów
Przesunięcie - translacja - obiektów
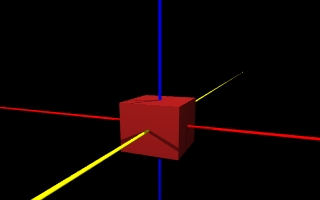
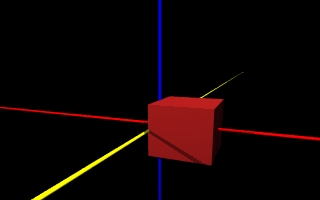
Każdą bryłę utworzoną gdziekolwiek w przestrzeni można przesunąć w dowolnym kierunku. Dokładniej mówiąc można ją przesunąć o dowolną ilośc jednostek w kierunku każdej z osi: X, Y i Z. Robimy to przy pomocy modyfikatora translate według wzoru:gdzie x, y i z określają o ile jednostek przesuwalmy obiekt w kierunku osi X, Y i Z. Oto przykład: Sześcian o boku a=4 umieszczony w początku układu współrzędnych przesuniemy o dwie jednostki w prawo, wzdłuż osi X.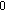
translate <x,y,z>
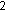
poniżej na rysunku po lewej stronie sześcian jest jeszcze w początku układu współrzędnych. po prawej stronie jest już przesunięty. Osie umieszczono dla orientacji.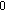
box
{
<-2,-2,-2>,<2,2,2>
texture {pigment{color Scarlet}}
translate <2,0,0> //w tym właśnie miejscu wpisane jest przesunięcie
}
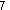
 |  |
Obrót obiektów
Każdy obiekt możemy obrócić o wybrany kąt względem każdej z osi. Zapis obrotu wygląda tak:gdzie:rotate <a,b,c>
a - kąt o jaki obracamy względem osi X,
b - kąt o jaki obracamy względem osi Y,
c - kąt o jaki obracamy względem osi Z.
Oczywiście możemy obrócić tylko zwględem jednej lub dwóch osi, wówczas pozostałe kąty sa równe 0. Obrócimy teraz nasz wyjściowy sześcian względem osi Y o 45 stopni. Definicja obiektu wyglądać będzie tak:
a końcowy efekt jest następujący:
box
{
<-2,-2,-2>,<2,2,2>>
rotate <0,0,45>
pigment {color Scarlet}
}
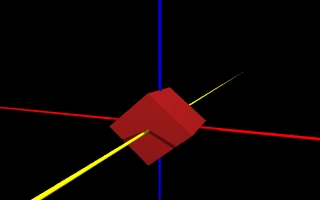
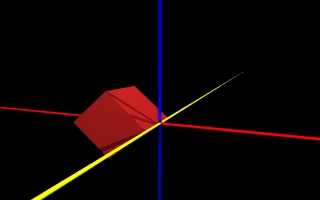 | 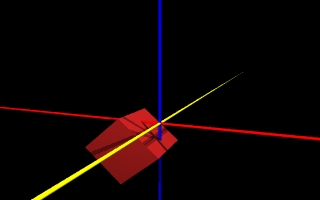 |
takich niespodzianek może być więcej, radzę uważać a w przypadku problemów najlepiej poćwiczyć w rzeczywistymi przedmiotami.
Powiększanie lub pomniejszanie czyli skalowanie bryły
Ostatnią w transformacji jest skalowanie. Każdą bryłę możemy powiększyć lub pomniejszyć wybrana ilość razy, względem dowolnej z osi. Wykonujemy to wpisując do definicji obiektu następujący kod:gdzie:
scale <a,b,c>
a - określa ile razy powiększyliśmy lub pomniejszyliśmy względem osi X
b - określa ile razy powiększyliśmy lub pomniejszyliśmy względem osi Y
c - określa ile razy powiększyliśmy lub pomniejszyliśmy względem osi Z
Dla przykładu powiększmy nasz sześcian dwukrotnie względem osi x. Definicja naszej bryły wygląda tak:
A tak to wygląda po zrenderowaniu:
box
{
<-2,-2,-2>,<2,2,2>
scale <2,1,1> //2 razy zwiększamy wzdłuż osi X, w pozostałych kierunkach bez zmian
pigment {color Scarlet}
}
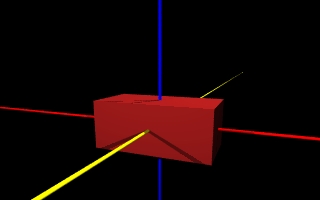
Przez wykorzystanie operacji boolowskih i transformacji do omówionych do tej pory brył możemy już uzyskać całkiem skomplikowane obiekty. Trzeba będzie jednak sporo pisać i często powtarzać te same fragmenty kodu. Niebawem pokaże jak tego uniknąć ale tymczasem proponuje wykonanie ilku obiektów w ramach ćwiczeń.
 | Palisada Pojedynczy pal powstał przez połaczenie walca i stożka przez operację union. Aby utworzyć palisadę skopiowałem kilkakrotnie kod definiujący pal i każdy z nich przesunąłem na odpowiednią odległośc w kierunku osi X za pomocą translate |
 | Kwiatek Płatki powstały z 6 walców, każdy kolejny jest obrócony w stosunku do poprzedniego o 30o za pomocą rotate. ¦rodek jest kulą umieszczoną w śroku układu współrzędnych |
 | Koło Koło powstało podobnie jak kwiat tylko walce zastąpiły tu prostopadłościany a obręcz jest wykonana za pomocą operacji difference w dwóch walców |